T. I. Kaltman, St. Petersburgská filiálka
Speciální astrofyzikální observatoře, Ruská akademie věd, Rusko, kti @saoran.spb.su
A. N. Koržavin, St. Petersburgská filiálka
Speciální astrofyzikální observatoře, Ruská akademie věd, Rusko, kor @saoran.spb.su
M. Klvaňa, Astronomický ústav Akademie
věd České republiky, observatoř Ondřejov, Česká republika, mklvana @asu.cas.cz
Abstrakt
Radiová měření dovolují za jistých
předpokladů určit velikost magnetického pole nad slunečními skvrnami. Popisujeme
metodu, která je používána pracovníky Speciální astrofyzikální observatoře
Ruské akademie věd při zpracovávání radiových dat, získaných radioteleskopem
RATAN-600, pracujícím na Kavkaze. Sama metoda měření nedovoluje určit výšku
ve sluneční atmosféře, které naměřené hodnoty magnetického pole odpovídají.
V této práci předkládáme čtyři metody
semiempirického modelování prostorové konfigurace vektorového magnetického
pole v symetrické skvrně, využívající dipólové aproximace a magnetografických
měření, s jejichž pomocí je možno hledanou výšku určit.
1. MECHANIZMUS ZÁŘENÍ A JEHO PROJEVY
Výsledky pozorování
ukazují, že aktivní oblasti, spojené se slunečními skvrnami, jsou v porovnání
s okolní koronou charakterizovány zvýšenými hodnotami koncentrace elektronů ![]() ,
intenzitou magnetického pole H a kinetickou teplotou
,
intenzitou magnetického pole H a kinetickou teplotou ![]() .
Jako základní mechanizmus záření nad slunečními skvrnami v centimetrové
a decimetrové oblasti radiových vln se uvádí cyklotronní záření tepelných
elektronů, pohybujících se po spirále, jejíž osa směřuje podél magnetických
siločar viz Železnjakov (1964). V takovém případě elektrony vyzařují na
frekvenci w:
.
Jako základní mechanizmus záření nad slunečními skvrnami v centimetrové
a decimetrové oblasti radiových vln se uvádí cyklotronní záření tepelných
elektronů, pohybujících se po spirále, jejíž osa směřuje podél magnetických
siločar viz Železnjakov (1964). V takovém případě elektrony vyzařují na
frekvenci w:
s=1,2….n – pořadové číslo harmonické frekvence,
![]() - gyrofrekvence,
- gyrofrekvence,
![]() -rychlost
světla,
-rychlost
světla, ![]() ,
,![]() - hmota a náboj elektronu.
- hmota a náboj elektronu.
Rovnice disperse pro homogenní magneticky aktivní plasmu (nebo nehomogenní – v aproximaci geometrické optiky) bez vlivu tepelných pohybů, určuje indexy lomu řádné a mimořádné vlny:
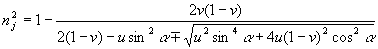 (2)
(2)
kde![]() ,
, ![]() ,
,
vlastní plasmová frekvence 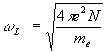 ,
,
![]() - úhel mezi vektorem magnetického
pole H
- úhel mezi vektorem magnetického
pole H
a normálou k vlnoploše.
Znaménko mínus a index j=1
odpovídá
mimořádné vlně, znaménko plus a index j=2
– řádné vlně. Řádná a mimořádná vlna mají opačnou polarizaci, která je
kruhová v případě šíření záření podél siločar magnetického pole. Směr kruhové
polarizace mimořádných vln souhlasí se směrem rotace elektronů v magnetickém
poli, v případě řádných vln je tomu naopak.
Oblast výstupu
záření je zdola omezena vrstvou, v níž je ![]() ,
protože pod touto vrstvou je index lomu imaginární a vlna rychle zaniká.
Při podélném šíření vlny (
,
protože pod touto vrstvou je index lomu imaginární a vlna rychle zaniká.
Při podélném šíření vlny (![]() ) vyplývá
ze vztahu (2), že hladina
) vyplývá
ze vztahu (2), že hladina ![]() odpovídá podmínce
odpovídá podmínce ![]() pro řádnou vlnu a
pro řádnou vlnu a ![]() pro vlnu
mimořádnou.
pro vlnu
mimořádnou.
V koronálním plasmatu
s maxvelovským rozložením rychlostí elektronů v nehomogenním magnetickém
poli se cyklotronní záření s frekvencí ![]() generuje v tenkých vrstvách, v nichž
generuje v tenkých vrstvách, v nichž ![]() splňuje podmínku (1).
splňuje podmínku (1).
Intensita a efektivní teplota vlastního záření, vycházejícího z termicky homogenní vrstvy (T=const.) magneticky aktivní plasmy do vákua se bude rovnat
![]() (3)
(3)
![]() (4)
(4)
kde I0 - je intenzita
záření v podmínkách termodynamické rovnováhy ve vákuu pro danou polarizaci
a ![]() - optická tloušťka zářící
vrstvy. Odsud je zřejmé, že pro
- optická tloušťka zářící
vrstvy. Odsud je zřejmé, že pro ![]() bude
bude![]() a v případě
a v případě ![]() bude
bude ![]() .
.
Výrazy pro optickou
tloušťku jsou komplikované, ale pro ![]() se
v případě (
se
v případě (![]() ) zjednodušují, zvláště
když index lomu
) zjednodušují, zvláště
když index lomu ![]() (tzn.
(tzn. ![]() ):
):
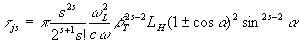 (5)
(5)
![]() -
poměr tepelné rychlosti elektronů k rychlosti světla,
-
poměr tepelné rychlosti elektronů k rychlosti světla,
![]() je charakteristický rozměr, v němž dochází ke změně hodnoty
je charakteristický rozměr, v němž dochází ke změně hodnoty ![]() podél paprsku.
podél paprsku.
Je důležité, že
optická tloušťka gyrorezonanční vrstvy pro mimořádnou vlnu ![]() při zachování ostatních podmínek bude vždy větší, než odpovídající hodnota
při zachování ostatních podmínek bude vždy větší, než odpovídající hodnota ![]() pro řádnou vlnu. Výpočty konkretních hodnot
pro řádnou vlnu. Výpočty konkretních hodnot ![]() ukazují,
že v podmínkách, typických pro aktivní oblasti korony, vrstvy s
ukazují,
že v podmínkách, typických pro aktivní oblasti korony, vrstvy s ![]() jsou průhledné pro oba druhy centimetrových vln (
jsou průhledné pro oba druhy centimetrových vln (![]() ).
).
Abychom získali
představu o pravděpodobném rozložení gyrorezonančních hladin nad skvrnou,
použijeme dipólovou aproximaci modelu unipolární skvrny. V tomto případě
se vrstvy s ![]() (
(![]() )
lokalizují tak, jak je znázorněno na obr.1.
)
lokalizují tak, jak je znázorněno na obr.1.
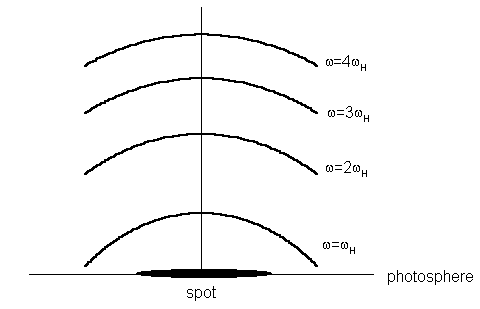
Obr. 1.: Uspořádání gyrorezonančních hladin nad oblastí skvrny.
Podíl mimořádného
záření z vrstev ![]() , v nichž
, v nichž ![]() a
a ![]() je celkem
nepodstatný: mimořádná vlna z hladiny
je celkem
nepodstatný: mimořádná vlna z hladiny![]() nevychází za hranice korony a je pohlcena v opticky tlusté vrstvě
nevychází za hranice korony a je pohlcena v opticky tlusté vrstvě![]() ,
která leži nad ní. S opticky tenkými vrstvami
,
která leži nad ní. S opticky tenkými vrstvami ![]() je spojeno záření, mající
je spojeno záření, mající ![]() .
Můžeme se proto domnívat, že při vyzařování mimořádné vlny hraje hlavní
roli vrstva
.
Můžeme se proto domnívat, že při vyzařování mimořádné vlny hraje hlavní
roli vrstva ![]() , jejíž teplota
, jejíž teplota ![]() je rovna kinetické teplotě této vrstvy
je rovna kinetické teplotě této vrstvy ![]() .
.
Pro mimořádné
vlny bude z těchže důvodů nepodstatné gyrorezonanční záření, vycházející
z vrstev ![]() a
a ![]() ,...
Roli efektivní zářici vrstvy hraje vrstva
,...
Roli efektivní zářici vrstvy hraje vrstva ![]() .
Vrstvy
.
Vrstvy ![]() , s vlnovými délkami
2 - 4 ?? leží v přechodové vrstvě mezi chromosférou
a koronou. Výše se nacházející vrstvě
, s vlnovými délkami
2 - 4 ?? leží v přechodové vrstvě mezi chromosférou
a koronou. Výše se nacházející vrstvě ![]() odpovídá vyšší kinetická teplota než vrstvě
odpovídá vyšší kinetická teplota než vrstvě ![]() ,
což se projevuje ve větší intenzitě mimořádné vlny. Pro kratší vlnové délky
,
což se projevuje ve větší intenzitě mimořádné vlny. Pro kratší vlnové délky ![]() se
zářící vrstvy posouvají do chladnější chromosféry, v níž efektivní teplota
klesá, pro delší vlnové délky se zářící vrstvy posouvají do horké, homogenní
korony, v níž se efektivní teploty řádné a mimořádné vlny vyrovnávají.
se
zářící vrstvy posouvají do chladnější chromosféry, v níž efektivní teplota
klesá, pro delší vlnové délky se zářící vrstvy posouvají do horké, homogenní
korony, v níž se efektivní teploty řádné a mimořádné vlny vyrovnávají.
2. MĚŘENÍ MAGNETICKÉHO POLE V OBORU RADIOVÝCH
VLN
2.1 POPIS METODY
Stoprocentní polarizace
na úseku křivky ![]() od vlnové délky
od vlnové délky ![]() téměř do maxima odpovídá absolutní převaze mimořádné vlny. Znamená to,
že řádná vlna (
téměř do maxima odpovídá absolutní převaze mimořádné vlny. Znamená to,
že řádná vlna (![]() ) se generuje
v chladnějších vrstvách chromosféry a naopak vrstva
) se generuje
v chladnějších vrstvách chromosféry a naopak vrstva ![]() ,
odpovídající mimořádné vlně, dosahuje výšek s vysokou koronální teplotou.
,
odpovídající mimořádné vlně, dosahuje výšek s vysokou koronální teplotou.
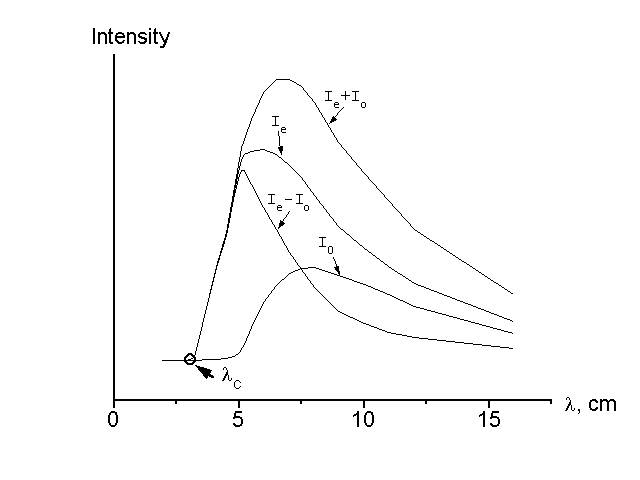
Obr. 2.: Rozložení záření řádné a mimořádné
vlny v závislosti na vlnové délce.
Se zmenšující
se vlnovou délkou se oblast, v níž se generuje mimořádná vlna posouvá do
nižších a chladnějších vrstev přechodové oblasti a chromosféry. Kritická
vlna ![]() , na níž je v tomto
případě pozorováno polarizované záření, odpovídá výstupu řádného záření
do korony v místě, v němž gyrorezonanční hladina třetí harmonické dosahuje
koronálních teplot.
, na níž je v tomto
případě pozorováno polarizované záření, odpovídá výstupu řádného záření
do korony v místě, v němž gyrorezonanční hladina třetí harmonické dosahuje
koronálních teplot.
Tady bude platit
![]() =3
=3 ![]() ,
,
a po dosazení získáme vztah mezi magnetickým polem a kritickou vlnovou délkou:
![]() (Gauss) (6)
(Gauss) (6)
2.2 APLIKACE METODY PRO RATAN-600
Pozorování RATAN-600 v oblasti 0.8 – 30 cm
s 5% rozlišovací schopností ve frekvencích a s vysokým prostorovým rozlišením
( 16'' na vlnové délce 1.7 cm) dovolují popisovanou
metodou určit magnetické pole nad slunečními skvrnami. Po identifikaci
zdroje nad vybranou skvrnou ve všech vlnových délkách je sestaveno spektrum
jeho polarizovaného záření.
Poté ve spektru vyhledáme nejkratší
vlnovou délku, na níž polarizované záření převyšuje hodnotu šumu a pro
tuto vlnovou délku a tři následující proložíme metodou nejmenších čtverců
spektrem přímku. Hledanou kritickou vlnovou délku ![]() nalezneme jako průsečík této přímky s osou vlnových délek. Magnetické pole
potom vypočítáme ze vzorce (6). Tento postup se provádí na RATAN-600 automaticky
při základním zpracování dat (Bogod a kol., 1999). Měření magnetických
polí radiových zdrojů se provádějí pravidelně od května 1999 a jsou
k disposici na Internetu na adrese http:\\www.sao.ru\~sun
nalezneme jako průsečík této přímky s osou vlnových délek. Magnetické pole
potom vypočítáme ze vzorce (6). Tento postup se provádí na RATAN-600 automaticky
při základním zpracování dat (Bogod a kol., 1999). Měření magnetických
polí radiových zdrojů se provádějí pravidelně od května 1999 a jsou
k disposici na Internetu na adrese http:\\www.sao.ru\~sun
Jistým problémem
uvedené metody je určení výšky, v níž bylo magnetické pole změřeno, neboť
sama metoda neumožňuje tento parametr určit. Navíc tato výška není konstantní,
ale mění se v závislosti na fyzikálních podmínkách. Proto jsme přistoupili
k trojdimenzionálnímu modelování vektorových magnetických polí ve skvrně,
jehož cílem je stanovení prostorové konfigurace magnetického pole nad skvrnou.
3. MODELOVÁNÍ VEKTOROVÝCH POLÍ
Pro ověření a upřesnění metody určování magnetických polí z radiových měření jsme použili semiempirický model, v němž jsme magnetické pole skvrny popsali osově symetrickou dipólovou aproximací.
![]() (7)
(7)
![]() (8)
(8)
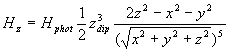 (9)
(9)
![]() (10)
(10)
![]() - komponenty vektoru magnetického
pole H
- komponenty vektoru magnetického
pole H
![]() - magnetické pole
ve
středu skvrny na úrovni fotosféry,
- magnetické pole
ve
středu skvrny na úrovni fotosféry,
![]() -
hloubka ponoření dipólu pod úroveň fotosféry.
-
hloubka ponoření dipólu pod úroveň fotosféry.
Optická tloušťka
vrstev, vyzařujících první čtyři harmonické girofrekvence byla pro oba
mody záření vypočtena podle vzorců (5) a efektivní teploty podle vzorce
(4). Abychom mohli provést srovnání vypočtených hodnot s hodnotami, měřenými
na RATAN-600, byla provedena dekonvoluce získaného rozložení intenzity
záření se směrovou charakteristikou přístroje. Ve spektru polarizovaného
záření byla v souladu s metodou, používanou na RATAN-600, vyhledána kritická
vlnová délka a podle vzorce (6) nalezena velikost magnetického pole.
Pro určení výšky
magnetického pole, změřeného přístrojem RATAN-600 jsme použili magnetografická
měření ondřejovského magnetografu a na základě dipólové aproximace jsme
vypracovali následující metody výpočtu třídímenzionálního, osově symetrického
vektorového magnetického pole nad skvrnou.
A) Metoda nulové vertikální komponenty vektoru magnetického pole
![]() , (11)
, (11)
Pokud dipól ponoříme
pod fotosféru na hloubku zdip= z,
vypočtenou z rovnice (11), bude na úrovni fotosféry ve vzdálenosti R
od středu skvrny vektorové magnetické pole dipólu pouze horizontální. Poloměr
R
můžeme určit podle obrazu skvrny v kontinuu spektra, buď jako poloměr penumbry
Rp,
projektované na střed slunečního disku,
nebo podle Kawakami (1983) jako 1.3 násobek Rp
Z magnetografických
měření určíme amplitudu vektoru magnetického pole ve středu skvrny Hphot,
ze vzorce (11) zdip a dosazením
do vzorců (7) – (10) vypočítáme vektorové magnetické pole nad skvrnou.
(Nula souřadnicového systému je ve středu dipólu a fotosféra ve výši zdip
nad ním.)
Vzhledem k tomu,
že u této metody existuje jednoznačný vztah mezi poloměrem skvrny a hloubkou
dipólu, můžeme konfiguraci magnetického pole nad skvrnou měnit jen změnou
poloměru
R. Rozbíhavost svazku
magnetického pole v prostoru je tak jednoznačně dána vzhledem magnetického
pole ve fotosféře. Výšku oblasti spodní korony pak určíme jako místo, v
němž se shodují hodnoty magnetického pole dipólu a radioastronomického
měření magnetického pole Ratanem.
B) Metoda izočar
Tato metoda
vychází z principu fitování izočar magnetického pole změřeného magnetografem
ve skvrně izočarami, vypočtenými na základě dipólové aproximace pro fotosféru.
Opět vycházíme z naměřených hodnot Hphot a volným
parametrem je zde hloubka dipólu zdip,
s jejíž pomocí můžeme vyhledat nejvhodnější konfiguraci obou typů izočar.
Vlastnosti této
metody jsou podobné, jako metody A), hodnoty magnetografických měření jsou
však více homogenizovány.
C) Metoda volby hloubky ponoření dipólu
Předcházející dvě metody obsahují pevnou vazbu mezi velikostí skvrny a hloubkou ponoření dipólu. Při analýze vlivu horizontálního proudění plasmy ve skvrně na konfiguraci jejího vektorového pole však potřebujeme hloubku ponoření dipólu nezávisle měnit. Úpravou vzorců (7) – (10) pro x=0 a y=0 dostaneme následující závislost intenzity magnetického pole Hh na výšce h nad fotosférou podél vertikální osy skvrny z:
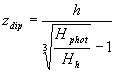 (12)
(12)
Ze vzorce (12) je zřejmé, že čím větší je hloubka dipólu zdip, tím větší je pro tutéž hodnotu Hh výška h nad fotosférou (jmenovatel je konstanta), to znamená, že při ponořování dipólu hlouběji pod fotosféru se ve směru vertikální osy skvrnyz gradient magnetického pole nad skvrnou zmenšuje. Tuto vlastnost je možno využít při fitování vertikálního průběhu magnetického svazku pole skvrny.
D) Metoda dvou spektrálních čar
ZÁVĚR
Uvedené metody používáme při modelování trojdimenzionálních vektorových magnetických polí nad symetrickými skvrnami. Některé z výsledků, získané na základě těchto metod, uvádíme v práci Kaltman a kol. ve sborníku této konference.
Poděkování:
Tato práce byla realizována díky grantovým projektům GAČR 205/97/0500, GAAV A3003903, RFBR 00-02-18017, INTAS – RFBR IR-97-1088 a Klíčovému projektu AVČR K1-003-601,
LITERATURA:
Železnjakov V.V., Radiozáření Slunce a
planet. Nauka, Moskva 1964.
Akhmedov Sh.B., Gelfreikh G.B., Bogod V.M., Korzhavin A.N., 1982:The
measurement of magnetic fields in the solar
atmosphere above sunspots using gyroresonance
emission, Solar Physics 79 (1982), 41-58
Kawakami, H.: 1983, Publ. Astron. Soc. Japan, 35, 459
Kaltman T. I., Klvaňa M., Bumba V.,: Modelování
prostorové konfigurace magnetického pole v symetrické skvrny na základě
optických a radiových
pozorování, Sborník této konference
Bogod V.M., Garaimov V.I., Komar N.P., Korzhavin A.N. , 1999 Ratan-600.
Upgrade and development of software for
presentation of the data, Proceedings of The
9th Europen Meeting on Solar Physics, Florence, Italy (ESA SP-448,
Vol. 2,
p. 1253